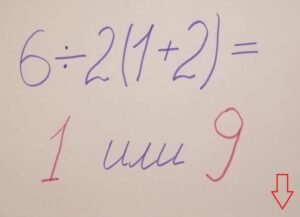
Задача, которая разорвала интернет на два лагеря! 😱 Даже профессора не могут договориться: 6:2(1+2) = ? Ответ удивит вас — и возможно, вы решали неправильно всю жизнь!

📌 Задача, которая разделила учёный мир: 6:2(1+2) = ?

Кажется, это просто арифметика… но ответ до сих пор вызывает споры! Подробности — в комментариях 👇👇👇

⸻

Эта задача — не просто школьный пример. Это уравнение взорвало интернет и спровоцировало настоящую математическую войну между физиками, математиками и даже учителями младших классов.

🔍 Вопрос простой на первый взгляд:
Чему равно выражение: 6:2(1+2)?

Одни убеждены, что ответ — 1.
Другие с пеной у рта доказывают, что это 9.
Но кто же прав?

⸻

🔎 В чём загвоздка?

Проблема кроется в неоднозначности записи.
Если следовать классическим правилам арифметики, где действия деления и умножения равны по приоритету и выполняются слева направо, то:

6:2(1+2) = 6:2×3 = 3×3 = 9

Но если интерпретировать скобки как приоритетную группу, то получится:

6:2(1+2) = 6 : (2×3) = 6:6 = 1

Так кто же прав — сторонники «единицы» или «девятки»?

🤯 Математики против физиков

Математики чаще склоняются ко второму варианту (1), особенно если придерживаются строгости в расставлении скобок и корректной записи.

Физики же, привыкшие к формулам вроде 2mgh : 2gh, моментально видят знакомую конструкцию и решают её как:

(2mgh) : (2gh) = m

То есть воспринимают всё выражение целиком, а не отдельные элементы.

⸻

📝 Что говорят стандарты?

По ГОСТу и типографическим правилам:
• умножение желательно обозначать явно: a • b или a × b
• запись ab допустима только, если она читается однозначно

А в нашем случае однозначности нет. Это — ловушка, которая ставит под сомнение даже простейшую логику.

⸻

❗Вывод

Если выражение вызывает споры — значит оно неправильно составлено.
В математике всё должно быть однозначно, особенно когда речь идёт об обучении детей или проверке знаний.

🔻 Поэтому:
Правильный ответ зависит не от вычислений, а от того, как вы прочитали запись. И это делает задачу уникальной — она не проверяет математику, она проверяет мышление!